Ptolemy

Ptolemaic System

In his Dialogue Concerning the Two Chief World Systems, Ptolemaic and Copernican of 1632, Galileo attacked the world system based on the cosmology of Aristotle (384-322 BCE) and the technical astronomy of Ptolemy (ca. 150 CE).

In his books On the Heavens, and Physics, Aristotle put forward his notion of an ordered universe or cosmos. It was governed by the concept of place , as opposed to space, and was divided into two distinct parts, the earthly or sublunary region, and the heavens. The former was the abode of change and corruption, where things came into being, grew, matured, decayed, and died; the latter was the region of perfection, where there was no change. In the sublunary region, substances were made up of the four elements, earth, water, air, and fire. Earth was the heaviest, and its natural place was the center of the cosmos; for that reason the Earth was situated in the center of the cosmos. The natural places of water, air, and fire, were concentric spherical shells around the sphere of earth. Things were not arranged perfectly, and therefore areas of land protruded above the water. Objects sought the natural place of the element that predominated in them. Thus stones, in which earth predominated, move down to the center of the cosmos, and fire moves straight up. Natural motions were, then, radial, either down or up. The four elements differed from each other only in their qualities. Thus, earth was cold and dry while air was warm and moist. Changing one or both of its qualities, transmuted one element into another. Such transmutations were going on constantly, adding to the constant change in this sublunary region.

Ptolemy

The heavens, on the other hand, were made up of an entirely different substance, the aether [1] or quintessence (fifth element), an immutable substance. Heavenly bodies were part of spherical shells of aether. These spherical shells fit tightly around each other, without any spaces between them, in the following order: Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, fixed stars. Each spherical shell (hereafter, simply, sphere) had its particular rotation, that accounted for the motion of the heavenly body contained in it. Outside the sphere of the fixed stars, there was the prime mover (himself unmoved), who imparted motion from the outside inward. All motions in the cosmos came ultimately from this prime mover. The natural motions of heavenly bodies and their spheres was perfectly circular, that is, circular and neither speeding up nor slowing down.

It is to be noted about this universe that everything had its natural place, a privileged location for bodies with a particular makeup, and that the laws of nature were not the same in the heavenly and the earthly regions. Further, there were no empty places or vacua anywhere. Finally, it was finite: beyond the sphere of the fixed stars and the prime mover, there was nothing, not even space. The cosmos encompassed all existence.

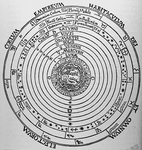Christian Aristotelian Cosmos. From Peter Apian, Cosmographia [click for larger image]

Now, ingenious as this cosmology was, it turned out to be unsatisfactory for astronomy. Heavenly bodies did, in fact, not move with perfect circular motions: they speeded up, slowed down, and in the cases of the planets even stopped and reversed their motions. Although Aristotle and his contemporaries tried to account for these variations by splitting individual planetary spheres into component spheres, each with a component of the composite motion, these constructions were very complex and ultimately doomed to failure. Furthermore, no matter how complex a system of spheres for an individual planet became, these spheres were still centered on the Earth. The distance of a planet from the Earth could therefore not be varied in this system, but planets vary in brightness, a variation especially noticeable for Venus, Mars, and Jupiter. Since in an unchangeable heaven variations in intrinsic brightness were ruled out, and since spheres did not allow for a variation in planetary distances from the Earth, variations in brightness could not be accounted for in this system.

Thus, although Aristotle's spherical cosmology had a very long life, mathematicians who wished to make geometrical models to account for the actual motions of heavenly bodies began using different constructions within a century of Aristotle's death. These constructions violated Aristotle's physical and cosmological principles somewhat, but they were ultimately successful in accounting for the motions of heavenly bodies. It is in the work of Claudius Ptolemy, who lived in the second century CE, that we see the culmination of these efforts. In his great astronomical work, Almagest, [2] Ptolemy presented a complete system of mathematical constructions that accounted successfully for the observed motion of each heavenly body.

Ptolemy used three basic constructions, the eccentric, the epicycle, and the equant. An eccentric construction is one in which the Earth is placed outside the center of the geometrical construction. Here, the Earth, E, is displaced slightly from the center, C, of the path of the planet. Although this construction violated the rule that the Earth was the center of the cosmos and all planetary motions, the displacement was minimal and was considered a slight bending of the rule rather than a violation. The eccentric in the figure below is fixed; it could also be made movable. In this case the center of the large circle was a point that rotated around the Earth in a small circle centered on the Earth. In some constructions this little circle was not centered in the Earth.

The second construction, the epicycle, is geometrically equivalent to the simple movable eccentric. In this case, the planet moved on a little circle the center of which rotated on the circumference of the large circle centered on the on theEarth. When the directions and speeds of rotation of the epicycle and large circle were chosen appropriately, the planet, as seen from the Earth, would stop, reverse its course, and then move forward again. Thus the annual retrograde motion of the planets (caused, in heliocentric terms by the addition of the Earth's annual motion to the motion of the planet) could roughly be accounted for.

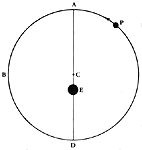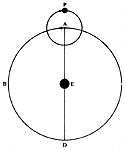Eccentric, epicycle, and equant. From Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution. [click each for larger image]

But these two constructions did not quite bring the resulting planetary motions within close agreement with the observed motions. Ptolemy therefore added yet a third construction, the equant. In this case, the center of construction of the large circle was separated from the center of motion of a point on its circumference, as shown below, where C is the geometrical center of the large circle (usually called in these constructions the excentric circle) but the motion of the center of the epicycle, P (middle figure), is uniform about Q, the equant point (righthand side figure).

Ptolemy combined all three constructions in the models of the planets, Sun, and Moon. A typical construction might thus be as in the picture below, where E is the Earth, C the geometric center of the eccentric circle, Q the equant point, F the center of the epicycle, and P the planet. As mentioned before, the eccentric was often not fixed but moved in a circle about the Earth or another point between the Earth and the equant point.

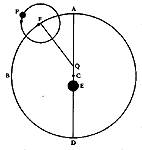Typical Ptolemaic planetary model(From Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution.) [click for larger image]

With such combinations of constructions, Ptolemy was able to account for the motions of heavenly bodies within the standards of observational accuracy of his day. The idea was to break down the complex observed planetary motion into components with perfect circular motions. In doing so, however, Ptolemy violated the cosmological and physical rules of Aristotle. The excentric and epicycle meant that planetary motions were not exactly centered on the Earth, the center of the cosmos. This was, however, a "fudge" that few objected to. The equant violated the stricture of perfect circular motion, and this violation bothered thinkers a good deal more. Thus, in De Revolutionibus (see Copernican System), Copernicus tells the reader that it was his aim to rid the models of heavenly motions of this monstrous construction.

Aristotelian cosmology and Ptolemaic astronomy entered the West, in the twelfth and thirteenth centuries, as distinct textual traditions. The former in Aristotle's Physics and On the Heavens and the many commentaries on these works; the latter in the Almagest and the technical astronomical literature that had grown around it, especially the work of Islamic astronomers working in the Ptolemaic paradigm. In the world of learning in the Christian West (settled in the universities founded around 1200 CE), Aristotle's cosmology figured in all questions concerned with the nature of the universe and impinged on many philosophical and theological questions. Ptolemy's astronomy was taught as part of the undergraduate mathematical curriculum only and impinged only on technical questions of calendrics, positional predictions, and astrology.

Copernicus's innovations was therefore not only putting the Sun in the center of the universe and working out a complete astronomical system on this basis of this premise, but also trying to erase the disciplinary boundary between the textual traditions of physical cosmology and technical astronomy.

Notes:
[1] The traditional English spelling, aether, is used here to distinguish Aristotle's heavenly substance from the modern chemical substance, ether.
[2] The title is one given to this book by Islamic translators in the ninth century. Its original Greek title is Mathematical Syntaxis.

Sources: The Aristotelian cosmos is described in his Physics and On the Heavens, see The Complete Works of Aristotle: The Revised Oxford Translation, ed. Jonathan Barnes, 2 vols. (Princeton: Princeton University Press, 1984). On the relationship between Greek cosmology and astronomy, see B. R. Goldstein and A. C. Bowen, "A New View of Early Greek Astronomy," Isis 74 (1983):330-40, and Thomas S. Kuhn, The Copernican Revolution (Cambridge: HArvard University Press, 1957. The best translation of the Almagest is Ptolemy's Almagest, tr. G. J. Toomer (London: Duckworth; New York: Springer Verlag, 1984). Godd expositions of the technical details of the Ptolemaic System can be found in Olaf Pedersen, A Survey of the Almagest (Odense: Odense University Press, 1974); Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution (New York: Dover, 1990); and Olaf Pedersen and Mogens Pihl, Early physics and astronomy : a historical introduction (London : MacDonald and Janes ; New York : American Elsevier, 1974; 2nd ed. Cambridge: Cambridge University Press, 1993). On Medieval cosmology and astronomy, see Edward Grant, "Cosmology," in Science in the Middle Ages, ed. David C. Lindberg (Chicago: University of Chicago Press, 1984), pp. 265-302; and Olaf Pedersen, "Astronomy," ibid, pp. 303-37. For an account of Aristotelian cosmology and Ptolemaic astronomy in the period leading up to Galileo's discoveries, see James M. Lattis, Between Copernicus and Galileo: Christoph Clavius and the Collapse of Ptolemaic Cosmology (Chicago: University of Chicago Press, 1994).